Exploring Hopfield Networks

Hopfield Networks are associative memories concerned with the storage and retrieval of data using a Lyapunov function ("energy function"). A Hopfield Network's memories are stored at local minima of this energy function. Given an initial data point, Hopfield Networks retrieve memories (perform "inference") by explicitly descending the energy (following the negative gradient of the energy). This inference process is a dynamical system that is guaranteed to converge to the fixed points ("memories").

In the exploratory spirit of this workshop, we have built a Hopfield Network demo that runs live in your web browser. The data stored in the network are the headshots of each person mentioned on the landing page. The animation below has two states:

  1. the selected person (the "label")
  2. the currently displayed image (the "dynamic state")

At every step, we display the recent history of energy values as a lineplot alongside a 2-D PCA projection of the current dynamic state (image). Watch as the dynamic state moves around the energy landscape characterized by local minima at each person!

The animation runs continously, taking small steps down the predicted energy of each (label, dynamic state) pair. If it looks like the animation stops running when the picture is clear, it is only because we have reached the appropriate local minimum of the energy: the model is still subtracting the energy gradient from the image (it so happens that the energy gradient is zero when the dynamic state equals the original headshot). See below for a more technical description of the demo.

The Anatomy of our Hopfield Network

An Associative Memory is a dynamical system that is concerned with the memorization and retrieval of data.

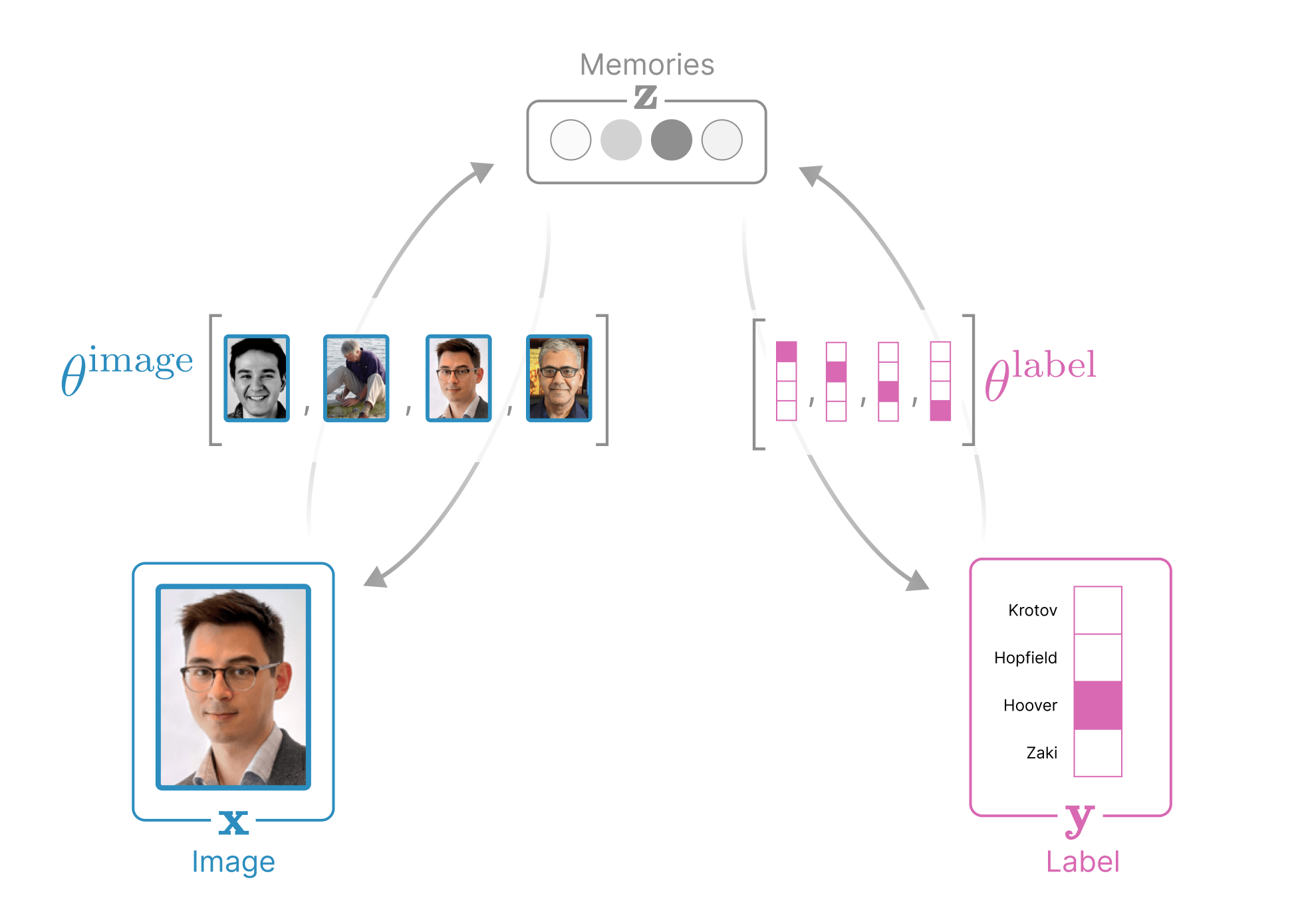
The structure of our data in the demo above is a collection of (image, label) pairs, where each image variable x∈R3Npixels{x \in \mathbb{R}^{3N_\mathrm{pixels}}} is represented as a rasterized vector of the RGB pixels and each label variable y∈RNpeople{y \in \mathbb{R}^{N_\mathrm{people}}} identifies a person and is represented as a one-hot vector. Our Associative Memory additionally introduces a third, hidden variable for the memories z∈RNmemories{z \in \mathbb{R}^{N_\mathrm{memories}}}.

In Associative Memories, each of these variables has both an internal state that evolves in time and an axonal state (an isomorphic function of the internal state) that influences how the rest of the network evolves. This terminology of internal/axonal is inspired by biology, where the "internal" state is analogous to the internal current of a neuron (other neurons don't see the inside of other neurons) and the "axonal" state is analagous to a neuron's firing rate (a neuron's axonal output is how it signals to other neurons). We denote the internal state of a variable with a hat: (i.e., variable x{x} has internal state x^{\hat{x}}, y{y} has internal state y^{\hat{y}}, and z{z} has internal state z^{\hat{z}}).

Dynamic variables in Associative Memories have two states: an internal state and an axonal state.

We call the axonal state the activations and they are uniquely defined by our choice of a scalar and convex Lagrangian function on that variable (see Krotov (2021), Krotov & Hopfield (2021), and Hoover et al. (2022) for more details). Specifically, in this demo we choose

Lx(x^)≜12∑ix^i2Ly(y^)≜log⁡∑kexp⁡(y^k)Lz(z^)≜1βlog⁡∑μexp⁡(βz^μ)\begin{align*} L_x(\hat{x}) \triangleq& \frac{1}{2} \sum\limits_i \hat{x}_i^2\\ L_y(\hat{y}) \triangleq& \log \sum\limits_k \exp (\hat{y}_k)\\ L_z(\hat{z}) \triangleq& \frac{1}{\beta} \log \sum\limits_\mu \exp(\beta \hat{z}_\mu) \end{align*}

These Lagrangians dictate the axonal states (activations) of each variable.

x=∇x^Lx=x^y=∇y^Ly=softmax(y^)z=∇z^Lz=softmax(βz^)\begin{align*} x &= \nabla_{\hat{x}} L_x = \hat{x}\\ y &= \nabla_{\hat{y}} L_y = \mathrm{softmax}(\hat{y})\\ z &= \nabla_{\hat{z}} L_z = \mathrm{softmax}(\beta \hat{z}) \end{align*}

The Legendre transform of the Lagrangian defines the energy of each variable.

Ex=∑ix^ixi−LxEy=∑ky^kyk−LyEz=∑μz^μzμ−Lz\begin{align*} E_x &= \sum\limits_i \hat{x}_i x_i - L_x\\ E_y &= \sum\limits_k \hat{y}_k y_k - L_y\\ E_z &= \sum\limits_\mu \hat{z}_\mu z_\mu - L_z\\ \end{align*}

All variables in Associative Memories have a special Lagrangian function that defines the axonal state and the energy of that variable.

In the above equations, β>0{\beta > 0} is an inverse temperature that controls the "spikiness" of the energy function around each memory (the spikier the energy landscape, the more memories can be stored). Each of these three variables is dynamic (evolves in time). The convexity of the Lagrangians ensures that the dynamics of our network will converge to a fixed point.

How each variable evolves is dictated by that variable's contribution to the global energy function Eθ(x,y,z){E_\theta(x,y,z)} (parameterized by weights θ{\theta}) that is LOW when the image x{x}, the label y{y}, and the memories z{z} are aligned (look like real data) and HIGH everywhere else (thus, our energy function places real-looking data at local energy minima). In this demo we choose an energy function that allows us to manually insert memories (the (image,label) pairs we want to show) into the weights θ={θimage∈RNmemories×3Npixels,    θlabel∈RNmemories×Npeople}{\theta = \left\{\theta^\mathrm{image} \in \mathbb{R}^{N_\mathrm{memories} \times 3N_\mathrm{pixels}},\;\; \theta^\mathrm{label} \in \mathbb{R}^{N_\mathrm{memories} \times N_\mathrm{people}}\right\}}. As before, let μ={1,…,Nmemories}{\mu = \left\{1,\ldots,N_\mathrm{memories} \right\}}, i={1,…,3Npixels}{i = \left\{ 1,\ldots,3N_\mathrm{pixels} \right\}} and k={1,…,Npeople}{k = \left\{1,\ldots,N_\mathrm{people} \right\}}. The global energy function in this demo is

Eθ(x,y,z)=Ex+Ey+Ez+12[∑μzμ(∑iθμiimage−xi)2−12∑ixi2]−λ∑μ∑kzμθμklabelyk=Ex+Ey+Ez+Exz+Eyz\begin{align} E_\theta(x, y, z) &= E_x + E_y + E_z + \frac{1}{2} \left[ \sum\limits_\mu z_\mu (\sum\limits_i \theta^\mathrm{image}_{\mu i} - x_i)^2 - \frac{1}{2} \sum\limits_i x_i^2\right] - \lambda \sum\limits_{\mu} \sum\limits_k z_\mu \theta^\mathrm{label}_{\mu k} y_k\\ &= E_x + E_y + E_z + E_{xz} + E_{yz} \end{align}

We introduce λ>1{\lambda > 1} to encourage the dynamics to align with the label.

Associative Memories can always be visualized as an undirected graph.

Every associative memory can be understood as an undirected graph where nodes represent dynamic variables and edges capture the (often learnable) alignment between dynamic variables. Notice that there are five energy terms in this global energy function: one for each node (Ex{E_x}, Ey{E_y}, Ez{E_z}), and one for each edge (Exz{E_{xz}} captures the alignment between memories and our image and Eyz{E_{yz}} captures the alignment between memories and our label). See the diagram below for the anatomy of this network.

Graph depcition of our Demo

In fact, every associative memory can be understood as an undirected graph where nodes represent dynamic variables and edges capture the (often learnable) alignment between dynamic variables. In our energy function, we have three nodes and two edges:

  • Image node x{x} representing the state of our image
  • Label node y{y} representing the state of our label
  • Hidden node z{z} representing the memories
  • Edge (x,z){(x,z)} capturing the alignment of the presented image to our memories
  • Edge (y,z){(y,z)} capturing the alignment of the presented label to our memories

where β>0{\beta > 0} is an inverse temperature that controls the "spikiness" of the energy function around each memory (the spikier the energy landscape, the more memories can be stored) and we introduce λ>1{\lambda > 1} to encourage the dynamics to align with the label. We use L2 similarity   L2(a,b)=−∑j(aj−bj)2{\;\mathrm{L2}(a,b) = - \sum\limits_j (a_j - b_j)^2} to capture the alignment of images to the memories stored in θimage{\theta^\mathrm{image}} and cosine similarity   cossim(a,b)=∑jajbj{\;\mathrm{cossim}(a,b) = \sum\limits_j a_j b_j} (where ∣∣a∣∣1=∣∣b∣∣1=1{||a||_1 = ||b||_1 = 1}) to capture the alignment of labels to memories stored in θlabel{\theta^\mathrm{label}}.

It is actually convenient to define a third dynamic variable zμ≜−∑i(θμiimage−xi)2+λ∑kθμklabelyk{z_\mu \triangleq -\sum\limits_{i} (\theta^{\mathrm{image}}_{\mu i} - x_i)^2 + \lambda \sum\limits_{k} \theta^\mathrm{label}_{\mu k} y_k } that captures the similarity of (x,y){(x,y)} to the μ{\mu}th memory (zμ{z_\mu} is dynamic in the sense that it evolves in time as a function of x{x} and y{y}). This allows us to reduce visual clutter of the energy function to

This global energy function Eθ(x,y,z){E_\theta(x,y,z)} turns our images, labels, and memories into dynamic variables whose internal states evolve according to the following differential equations:

τxdx^idt=−∂Eθ∂xi=∑μzμ(θμiimage−xi)τydy^kdt=−∂Eθ∂yk=λ∑μzμθμklabel−y^kτzdz^μdt=−∂Eθ∂zμ=−12∑i(θμiimage−xi)2+λ∑kθμklabelyk−z^μ\begin{align*} \tau_x \frac{d\hat{x}_i}{dt} &= -\frac{\partial E_\theta}{\partial x_i} = \sum\limits_\mu z_\mu \left( \theta^\mathrm{image}_{\mu i} - x_i \right)\\ \tau_y \frac{d\hat{y}_k}{dt} &= -\frac{\partial E_\theta}{\partial y_k} = \lambda \sum\limits_\mu z_\mu \theta^\mathrm{label}_{\mu k} - \hat{y}_k\\ \tau_z \frac{d\hat{z}_\mu}{dt} &= -\frac{\partial E_\theta}{\partial z_\mu} = - \frac{1}{2} \sum\limits_i \left(\theta^\mathrm{image}_{\mu i} - x_i \right)^2 + \lambda \sum\limits_k \theta^\mathrm{label}_{\mu k} y_k - \hat{z}_\mu\\ \end{align*}

where τx,τy,τz{\tau_x, \tau_y, \tau_z} define how quickly the states evolve.

The variables in Associative Memories always seek to minimize their contribution to a global energy function.

Note that in the demo we treat our network as an image generator by clamping the labels (forcing dy^dt=0{\frac{d\hat{y}}{dt} = 0}). We could similarly use the same Associative Memory as a classifier by clamping the image (forcing dx^dt=0{\frac{d\hat{x}}{dt} = 0}) and allowing only the label to evolve.